Центробежная противоточная мельница с классификацией материала в зоне загрузки
РЕФЕРАТ. В статье рассмотрена конструкция центробежной противоточной мельницы с классификацией материала в зоне загрузки. Отделение мелкой фракции частиц от крупной перед соударением частиц в лобовых и пересекающихся потоках в тангенциальном канале мельницы позволит повысить эффективность измельчения. Функцию отделения мелкой фракции частиц от крупной выполняют радиально расположенные на дисках мельницы полукруглые канавки. Установлено, что условие, когда мелкие частицы попадают в эти канавки, определяется угловым размером установки криволинейных лопаток на диске мельницы. Исходя из этого получена аналитическая зависимость между глубиной канавки и конструктивнотехнологическими параметрами мельницы, позволяющая определить значение данного угла. Данная зависимость определяет условие, когда частица материала преодолевает радиально расположенную канавку. Результаты настоящей статьи могут быть использованы при конструировании центробежных противоточных мельниц, а также в учебном процессе.
Ключевые слова: центробежная противоточная мельница, криволинейная лопатка, радиальная канавка, частота вращения, горизонтальный диск, частица материала.
Keywords: centrifugal countercurrent mill, curved blade, radial groove, rotation speed, horizontal disc, material particle.
Один из видов установок, в которых измельчаются сыпучие материалы с повышенной твердостью и абразивностью, — центробежные противоточные мельницы. В таких измельчителях частицы материала механически разгоняются, чтобы затем они соударялись во встречных и пересекающихся потоках [1—3].
Центробежные противоточные мельницы имеют следующие достоинства: сравнительно малые габариты, простоту конструкции, возможность регулировать гранулометрический состав готового продукта, сравнительно малую установленную мощность [4].
Один из недостатков таких мельниц — отсутствие классификации частиц материала по крупности при их движении на поверхности разгонных дисков [5].
Поэтому создание центробежных противоточных мельниц, в которых происходит селективное самоизмельчение частиц во встречных и пересекающихся потоках, является актуальной задачей.
В данной статье описана конструкция центробежной противоточной мельницы (рис. 1), на горизонтальных дисках 1 которой жестко закреплены криволинейные вертикальные лопатки 2 и выполнены радиально расположенные канавки 3 полукруглого поперечного сечения для разделения частиц крупной и мелкой фракции перед их вылетом в тангенциальный канал 5. Для выгрузки готового продукта в центре тангенциального канала 5 расположен разгрузочный патрубок 6.
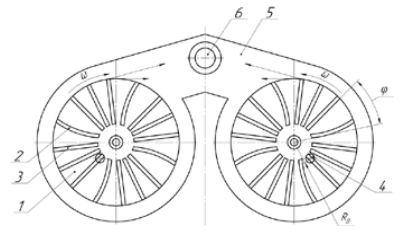
Рис. 1. Центробежная противоточная мельница: 1 — горизонтальные диски, 2 — криволинейные лопатки, 3 — радиальные канавки, 4 — вертикальные загрузочные патрубки, 5 — тангенциальный канал, 6 — разгрузочный патрубок
Для согласования пропускной способности Q1 бункера и вертикального загрузочного патрубка Q2, площадь поперечного сечения которого имеет форму эллипса с полуосями а и b, должно выполняться соотношение Q1 = Q2 [6, 7].
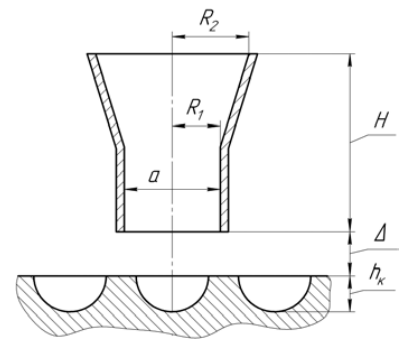
Рис. 2. Узел загрузки горизонтального диска
На основании конфигурации узла загрузки горизонтального диска (рис. 2) выражения для определения пропускной способности бункера Q1 и вертикального загрузочного патрубка Q2 выглядят следующим образом:
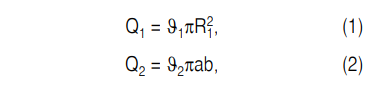
где ϑ1 — скорость истечения частиц материала из бункера, равная [4]:
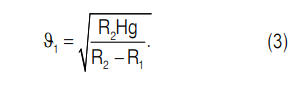
В уравнении (3): R1 и R2 — соответственно радиусы выпускного отверстия и верхнего основания конического бункера, H — высота конического бункера.
На основании (1) и (2) находим:
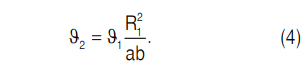
Согласно соотношению (4), время t1, необходимое для загрузки мелких частиц в радиальную канавку 3 полукруглого поперечного сечения радиусом r0 (r0 ≥ d/2, где d — диаметр частицы), определяется соотношением:
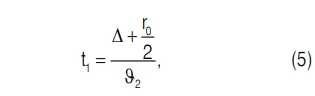
где Δ — расстояние от нижнего среза вертикального загрузочного патрубка 4 до верхней поверхности горизонтального диска 1.
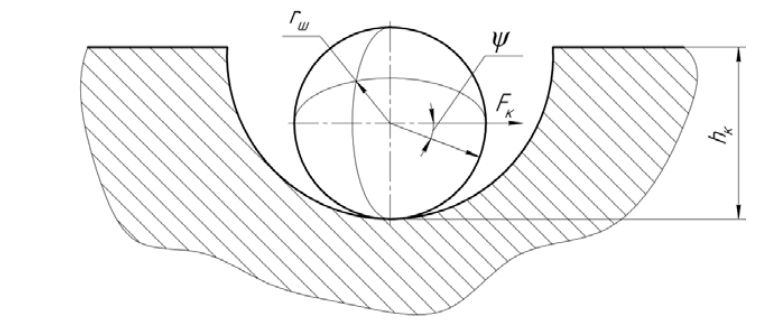
Рис. 3. Схема расположения частицы материала в радиальной канавке
Попав в радиально расположенную канавку 3, частица диаметром d/2 ≤ r0 начинает двигаться вдоль ее поверхности (рис. 3) со скоростью, равной
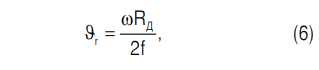
где RД — радиальное расстояние от оси вращения горизонтального диска до точки загрузки частиц, f — коэффициент трения частицы о поверхность радиальной канавки, ω — частота вращения горизонтального диска мельницы.
Время t2, необходимое для захвата криволинейной лопаткой, закрепленной на горизонтальном диске, крупных частиц материала, поступающих из вертикального загрузочного патрубка, определяется соотношением [8]:
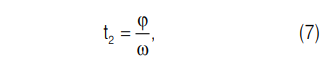
где φ — угол поворота криволинейной лопатки.
Чтобы частицы материала радиусом d/2 ≤ r0 могли попасть в радиально расположенную канавку, должно выполняться соотношение
![]()
На основании выражений (5), (7) и (8) получаем соотношение:
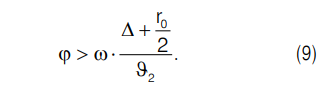
Выражение (9) определяет угловой размер установки криволинейной лопатки на горизонтальном диске центробежной противоточной мельницы.
Рассмотрим условие, когда сферическая частица материала преодолевает радиально расположенную канавку полукруглого поперечного сечения глубиной hk, расположенную на поверхности горизонтального диска 1. Роль рассматриваемого барьера выполняет внутренняя поверхность этой канавки.
Согласно расчетной схеме, представленной на рис. 3, частица материала сферической формы, имеющая радиус rш, преодолеет радиальную канавку при выполнении неравенства
![]()
Здесь M — абсолютная величина момента силы Fk, равная:
![]()
![]()
где Fk — модуль силы Кориолиса, Н; m — масса частицы материала, кг; ϑ3 — линейная скорость частицы в точке встречи с боковой поверхностью криволинейной лопасти, закрепленной на горизонтальном диске, м/с:
![]()
В неравенстве (10) Еn — потенциальная энергия, Дж:
![]()
где g — ускорение свободного падения, м/с2.
Подставляя (11) и (14) в неравенство (10) и учитывая (12) и (13), получаем
![]()
На основании рис. 3 рассчитываем
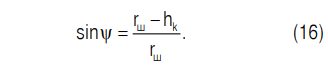
С учетом (16) неравенство (15) принимает вид:
![]()
Выражение (17) можно представить в виде
![]()
где
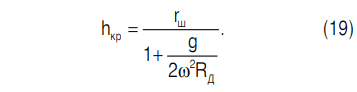
Таким образом, полученными соотношениями (18) и (19) определяются условия, когда частица материала может преодолеть радиально расположенную канавку полукруглого поперечного сечения (см. рис. 3).
Из уравнения (19) следует, что с увеличением частоты ω вращения горизонтального диска и радиуса частицы rш критическое (максимальное) значение глубины радиальной канавки возрастает по линейному закону.
ЛИТЕРАТУРА
1. Сиваченко Л.А. Современное технологическое машиностроение. Основные положения // Инженер-механик. 2010. № 4. С. 10—20.
2. Хинт И.А. Основы производства силикальцитных изделий. М.: Госстройиздат. 1962. 601 с.
3. Богданов В.С., Семикопенко И.А., Воронов В.П. Дезинтеграторы. Конструкции. Теория. Эксперимент. Белгород, 2016. 235 с.
4. Семикопенко И.А., Воронов В.П., Пензев П.П. Теоретические исследования скорости движения частиц материала вдоль поверхности ударного элемента мельницы дезинтеграторного типа // Изв. ВУЗов. Строительство. 2008. № 11. С. 93—96.
5. Товаров В.В., Оскаленко Г.Н. Исследование вылета частиц
из лопастных роторов центробежных измельчающих машин
// Госстройиздат. 1962. № 3. С. 64—91.
6. Бабичева И.В., Болдовская Т.Е. Справочник по математике
(в формулах, таблицах, рисунках). Омск, 2010. 148 с.
7. Bradley A.A., Freemantle A.J., Lloyd P.J. Developments in centrifugal milling // J. of the South African Inst. of Mining and Metallurgy. June 1974. Р. 379—387.
8. Богданов В.С., Семикопенко И.А., Масловская А.Н., Александрова Е.Б. Дезинтегратор с повышенными нагрузками на измельчаемый материал // Строительные и дорожные машины. 2009. № 5. С. 51—54.
| Автор: И.А. Семикопенко, В.П. Воронов, Д.А. Беляев |
| Рубрика: Оборудование и технология |
| Ключевые слова: центробежная противоточная мельница, криволи-нейная лопатка, радиальная канавка, частота вращения, горизонталь-ный диск, частица материала |




