Механика дробящей среды в шаровых барабанных мельницах с поперечно-продольным движением мелющих тел
РЕФЕРАТ. В статье рассматривается методика расчета кинематических параметров движения мелющих тел в шаровой барабанной мельнице с их поперечно-продольным перемещением. Получены математические зависимости, позволяющие рассчитать углы отрыва шара от внутренней поверхности барабана мельницы и наклонной межкамерной перегородки. Приведен анализ расчетов траектории движения и углов отрыва шара в течение цикла. Подтверждена интенсификация движения мелющих тел за счет их дополнительного продольного перемещения наклонной межкамерной перегородкой.
Ключевые слова: шаровая барабанная мельница, мелющие тела, шар, траектория движения, угол отрыва, сила давления, частота вращения.
Keywords: ball-tube mill, grinding bodies, ball, motion trajectory, separation angle, press force, rotation frequency.
Введение
Расчет кинематических, энергетических, динамических, скоростных параметров мелющей среды в шаровых барабанных мельницах, до настоящего времени, основан на применении теории Дэвиса, согласно которой шар до точки отрыва перемещается по круговой траектории вместе с барабаном мельницы, а затем, в точке отрыва, переходит на параболическую траекторию свободного падения, совершая измельчение ударом в точке падения [1—6]. При рассмотрении кинематики движения мелющих тел в шаровой барабанной мельнице в классической постановке вопроса физико-механические свойства измельчаемого материала не учитываются [2, 5, 7, 8].
В течение одного оборота барабана мельницы размер частиц и их физико–механические свойства изменяются в широких пределах. Исходный размер частиц 30—50 мм уменьшается в сотни раз и становится меньше 10 мкм. В связи с тем, что частицы разрушаются по дефектам структуры, наступает такой момент, когда частица уже не имеет дефектов и для ее разрушения требуется существенно бóльшая энергия. На каждом участке барабана мельницы находятся частицы, различающиеся по размерам в тысячи раз, что подтверждается диаграммами помола. Как показали наши собственные исследования и исследования других авторов, наличие в шаровой мельнице измельчаемого материала повышает потребляемую мощность привода мельницы не более чем на 15 % [1—6]. Существующие методики расчета потребляемой мощности привода дают погрешность до 60 %. Поэтому учет материала не только усложнит получение математических моделей, но и снизит их адекватность. В связи с этим при построении модели механики дробящей среды в мельнице с поперечно-продольным движением (ППД) мелющих тел мы также считаем нецелесообразным учитывать физико-механические свойства измельчаемого материала.
Зная параметры движения шара в течение цикла в мельнице с ППД мелющих тел, мы сможем рассчитать все основные кинематические, энергетические, технологические и конструктивные параметры мельницы. В нашей модели мы рассматриваем не один шар, а совокупность шаров, находящихся одновременно на расчетной траектории движения в течение одного цикла. При этом на шар в момент его отрыва от внутренней поверхности барабана действует не только сила давления барабана, но и продольная сила со стороны плоскости наклонной перегородки.
Здесь мы предлагаем принципиально новый подход при рассмотрении траектории движения шаров в течение цикла в мельнице с ППД мелющих тел. Рассчитав траекторию движения шара в неподвижной системе координат, в соответствии с теорией Дэвиса, мы вводим подвижную систему координат, расположенную в плоскости наклонной перегородки, и далее рассчитываем траекторию всей совокупности шаров при последовательном изменении положения этой перегородки [9].
Расчет угла отрыва шара, находящегося на наклонной межкамерной перегородке
В принятой расчетной системе координат (рис. 1) на шар, находящийся на наклонной межкамерной перегородке и вместе с тем контактирующий с внутренней поверхностью барабана мельницы, одновременно действуют вес шара (G), сила инерции (C), сила реакции барабана (Nб) и дополнительная сила реакции (NП) со стороны наклонной перегородки, направленная перпендикулярно плоскости перегородки.
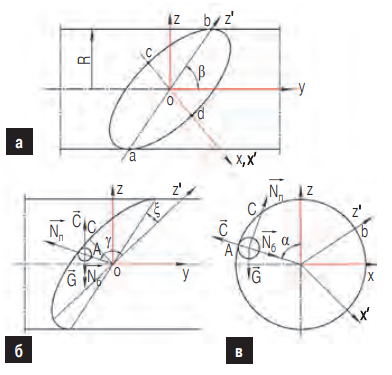
Рис. 1. Расчетная схема действующих сил в выбранной системе координат
Уравнение равновесия шара, находящегося на наклонной перегородке, имеет вид:
![]()
где Nб и NП — силы реакции барабана и наклонной перегородки соответственно, C — центробежная сила, G — вес шара.
В принятой неподвижной системе координат OXYZ (рис. 1) для расчета значений сил реакции барабана Nб и наклонной перегородки NП на шар получим уравнения:
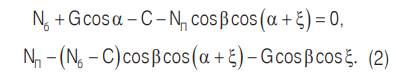
Данная система уравнений справедлива до того момента, пока шар движется вместе с барабаном, одновременно находясь на поверхности наклонной межкамерной перегородки.
Если сила Nб станет равной нулю, то шар оторвется от внутренней поверхности барабана, но продолжит свое движение вдоль поверхности наклонной межкамерной перегородки. Уравнения, описывающие его движение, примут вид:
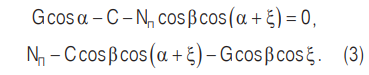
Cила реакции наклонной межкамерной перегородки рассчитывается по уравнению:
![]()
Если первой по времени станет равной нулю реакция NП со стороны наклонной перегородки, то шар оторвется от нее, и дальнейшее его движение будет описываться уравнениями:
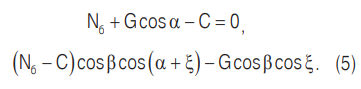
Если шар при последующем движении не упадет на наклонную перегородку, то его отрыв от внутренней поверхности барабана произойдет при значении угла, равном:
![]()
Таким образом, угол отрыва от внутренней поверхности барабана мельницы известен — он определяется по уравнению (6). Далее рассчитаем угол отрыва шара от барабана при его контакте с наклонной перегородкой. С этой целью мы получили уравнения, характеризующие положение шара на этой перегородке при его одновременном контакте с барабаном мельницы:
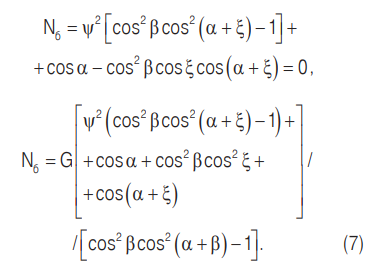
Уравнения (7) учитывают все основные факторы, влияющие на угол отрыва α: частоту ψ вращения барабана мельницы, угол β наклона перегородки и ее положение по отношению к шару.
Численное решение уравнений (7) позволяет получить любую из функций α (ξ, β, ψ), которые имеют синусоидальный характер, а, следовательно, им присуще наличие экстремумов. Из этого следует, что при изменении угла отрыва шара α от минимума до максимума за один оборот барабана мельницы, оснащенной наклонной межкамерной перегородкой, на каждом участке барабана мельницы каскадный режим работы мелющих тел изменяется на водопадный, при котором обеспечивается селективность измельчения в целом.
Однако характер движения мелющих тел описывается наиболее полно, если известно положение шара по отношению к наклонной перегородке в момент его отрыва от барабана мельницы. С этой целью мы ввели дополнительные относительные координаты OX’Z’ (рис. 1). В принятой системе координат угол γ определяет положение центра тяжести шара в момент его отрыва от барабана мельницы по отношению оси Z. Этот угол описывается уравнением γ (ξ, α, β).
Положение центра тяжести шара в неподвижной системе координат OXYZ в момент его отрыва от барабана мельницы описывается уравнениями:
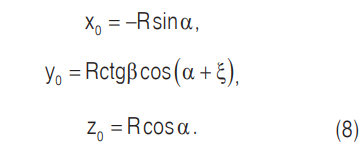
Введя еще одну подвижную ось Z’’, которая является проекцией оси Z’ на плоскость XOZ, получим:
![]()
Тогда в подвижной системе координат получаем следующее:
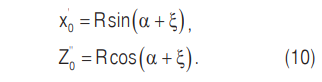
С учетом уравнений (9) и (10) координаты положения центра тяжести шара по отношению к наклонной перегородке в момент отрыва от барабана мельницы можно рассчитать следующим образом:
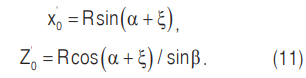
Исходя из расчетной схемы (рис. 1) и с учетом (11) имеем:
![]()
Исходя из уравнения (12), определим угол γ:
![]()
На рис. 2 представлены некоторые результаты численного решения уравнений γ (α, ξ, β) и α (ψ, β, ξ). Наибольший интерес представляют функции α, γ (ξ) при β и ψ = const. Характером графиков α (ξ), приведенных на рис. 2, и той же зависимости, полученной аналитически, полностью подтверждается наш вывод о существенном изменении кинетики шаровой загрузки в мельнице, оснащенной наклонной межкамерной перегородкой. В обычных шаровых барабанных мельницах угол отрыва шара от внутренней поверхности барабана в течение цикла не изменяется; при частоте вращения ψ, равной 0,76 ее критического значения, он составляет 54° и на графике отображается прямой, параллельной оси.
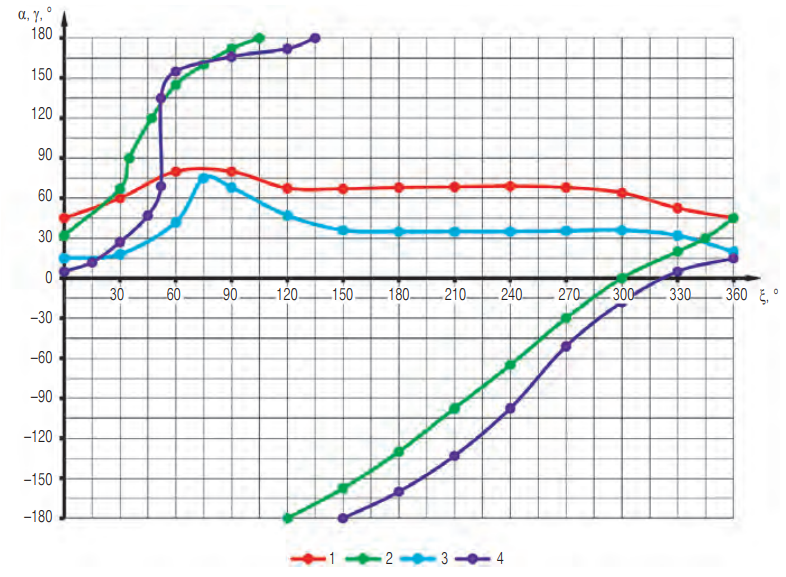
Рис. 2. Расчетные зависимости a(x) (1, 3) и g(x) (2, 4) при y = 0,76 и b = 45° (1, 2) и при y = 0,90 и b = 30° (3, 4)
В мельницах с наклонной межкамерной перегородкой этот угол изменяется в широких пределах (см. рис. 2). Например, при β = 30° и ψ = 0,9 угол отрыва шара изменяется от 15 до 89°, при β = 45° и ψ = 0,7 — от 35 до 80°. В обычной мельнице угол отрыва постоянен в течение цикла и равен соответственно 36 и 60°.
Отметим, что с увеличением частоты вращения барабана мельницы на всех участках траектории, кроме 60° < γ < 105°, высота подъема шара увеличивается, и энергия шаров соответственно возрастает.
Из данных рис. 2 следует, что на участке траектории движения мелющих тел, равном четверти оборота барабана мельницы, шары поднимаются на значительно бóльшую высоту, чем в обычных барабанных мельницах, и им сообщается бóльшая потенциальная энергия, которая обеспечивает бóльшую эффективность измельчения.
Данные рис. 2 также показывают, что наибольшая высота подъема мелющих тел соответствует такому взаимному расположению шара и наклонной перегородки, при котором точка А контакта шара с наклонной перегородкой находится в области 0° < γ < 105°. Этот аналитический вывод позволяет найти конструктивное решение, основанное на взаимном расположении наклонных межкамерных перегородок, максимальную высоту подъема мелющих тел по вcей длине барабана мельницы.
Выводы
При постоянной частоте вращения барабана мельницы и заданном угле наклона межкамерной перегородки наблюдается значительное изменение угла отрыва шара, что в целом существенно изменяет режим работы мелющих тел.
Во всем цикле движения шаров можно выделить три характерных режима их движения: 1) когда они поднимаются на бóльшую высоту, чем у обычных мельниц (это составляет четверть оборота барабана); 2) они поднимаются на меньшую высоту (около одной восьмой оборота барабана); 3) они имеют такой же угол отрыва, как и у шаров в обычных мельницах (около половины оборота). Наблюдается лавинообразный отрыв шаров от барабана мельницы, когда за небольшой промежуток времени на свободные траектории падения переходит около 30 % мелющих тел, находящихся в зоне расположения наклонной межкамерной перегородки.
Источник финансирования
Работа выполнена в рамках поддержанного Российским научным фондом проекта № 22—29—01438.
ЛИТЕРАТУРА
1. Дуда В. Цемент. М.: Стройиздат, 1981. 464 с.
2. Андреев С.Е., Зверевич В.В., Перов В.А. Дробление, измельчение и грохочение полезных ископаемых. М.: Недра, 1980. 415 с.
3. Крюков Д.К. Футеровка шаровых мельниц. М.: Машиностроение, 1965. 184 с.
4. Горобец В.И., Горобец Л.Ж. Новое направление работ по измельчению. М.: Недра, 1977. 183 с.
5. Богданов В.С., Шарапов Р.Р., Фадин Ю.М. Основы расчета машин и оборудования предприятий строительных материалов и изделий. Старый Оскол: ТНТ, 2013. 680 с.
6. Богданов В.С., Богданов Д.В., Семикопенко И.А. Процессы в производстве строительных материалов. Старый Оскол: ТНТ, 2018. 436 с.
7. Reichardt R., Wiechert W. Event driven algorithms applied to a high energy ball mill simulation // Granular Matter. 2007. Vol. 9, N 3—4. P. 251—266.
8. Лилу Ж., Кукарт М. Модернизация помольных мощностей ОАО «Гарадаг Цемент» // Цемент и его применение. 2012. № 5. С. 208—209.
9. Bogdanov V.S., Dontsova Y.A., Bogdanov N.E. Mechanics of the grinding media in ball mills with longitudinal and transverse motion of the grinding mtdia // ZKG Cement Lime Gypsum. 2019. Vol. 6. P. 15—24.
| Автор: В.С. Богданов, С.И. Анциферов, Д.В. Богданов, Е.А. Сычев |
| Рубрика: Оборудование и технология |
| Ключевые слова: шаровая барабанная мельница, мелющие тела, шар, траектория движения, угол отрыва, сила давления, частота вращения |




